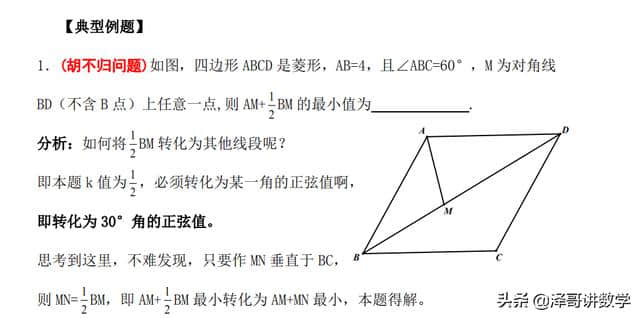
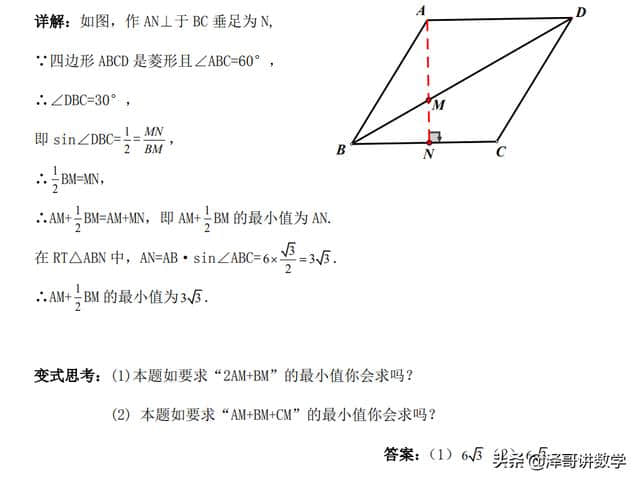
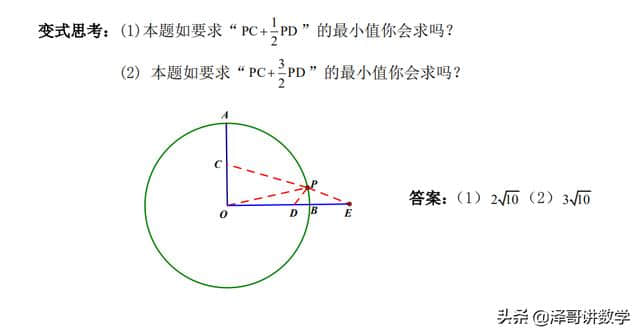
返回目录:美文欣赏
“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。当 k 值为 1
时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“饮马问题”模型
来处理,即可以转化为轴对称问题来处理。
而当 k 取任意不为 1 的正数时,若再以常规的轴对称思想来解决问题,则无
法进行,因此必须转换思路。
此类问题的处理通常以动点P所在图像的不同来分类,一般分为2类研究。
即点 P 在直线上运动和点 P 在圆上运动。
其中点 P 在直线上运动的类型称之为“胡不归”问题;
点 P 在圆周上运动的类型称之为“阿氏圆”问题。
本文将分别从这两类入手与大家共同探究线段最值问题的解决方案。
(一)点 P 在直线上运动 “胡不归”问题
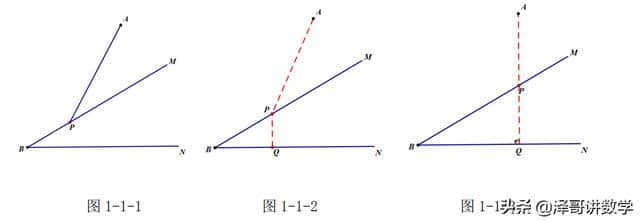
如图 1-1-1 所示,已知 sin∠MBN=k,点 P 为角∠MBN 其中一边 BM 上的一个动
点,点 A 在射线 BM、BN 的同侧,连接 AP,则当“PA+k·PB”的值最小时,P 点的
位置如何确定?
分析:本题的关键在于如何确定“k·PB”的大小,过点 P 作 PQ⊥BN 垂足为
Q,则 k·PB=PB·sin∠MBN=PQ,
∴本题求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值(如图 1-1-2),
即 A、P、Q 三点共线时最小(如图 1-1-3),本题得解。
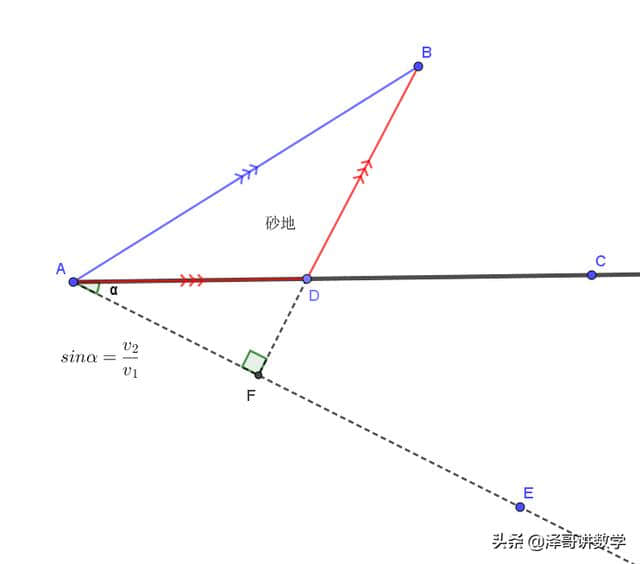
【数学故事】从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危
的消息后,便立即启程赶路。由于思乡心切,他只考虑了两点之间线段最短的原
理,所以选择了全是沙砾地带的直线路径 A→B(如图所示),而忽视了走折线虽
然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小
伙子失声痛哭。邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?
胡不归?…何以归”。这个古老的传说,引起了人们的思索,小伙子能否提前到
家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问
题”。
(二)点 P 在圆上运动 “阿氏圆”问题
如图所示 2-1-1,⊙O 的半径为 r,点 A、B 都在⊙O 外,P 为⊙O 上的动点,
已知 r=k·OB.连接 PA、PB,则当“PA+k·PB”的值最小时,P 点的位置如何确
定?
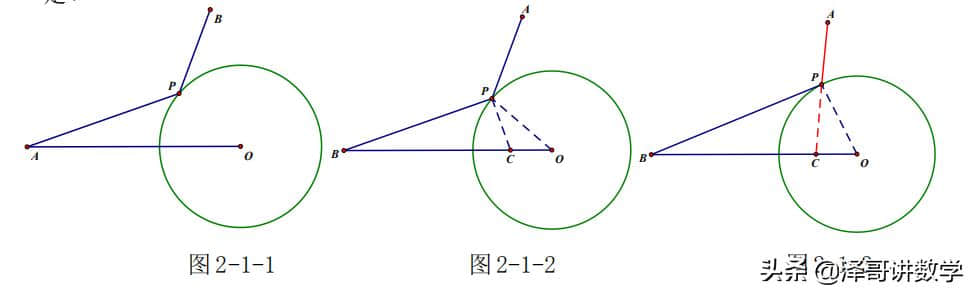
分析:本题的关键在于如何确定“k·PB”的大小,(如图 2-1-2)在线段 OB
上截取 OC 使 OC=k·r,则可说明△BPO 与△PCO 相似,即 k·PB=PC。
∴本题求“PA+k·PB”的最小值转化为求“PA+PC”的最小值,即 A、P、C
三点共线时最小(如图 2-1-3),本题得解。
【问题背景】阿氏圆又称阿波罗尼斯圆,已知平面上两点 A、B,则所有满足
PA=kPB(k≠1)的点 P 的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼
斯发现,故称“阿氏圆”。