「数学小专题」最值问题——胡不归问题

本文转载自： 赵桂芳名师工作室

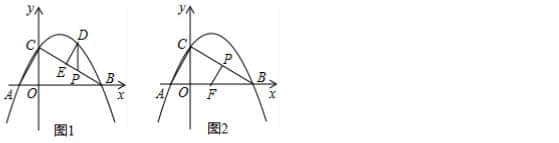
方法：以动点所在直线为对称轴，作定点的对称点.

（利用两点之间，线段最短）

方法：以动点所在直线为对称轴，作定点的对称点.

（利用垂线段最短）

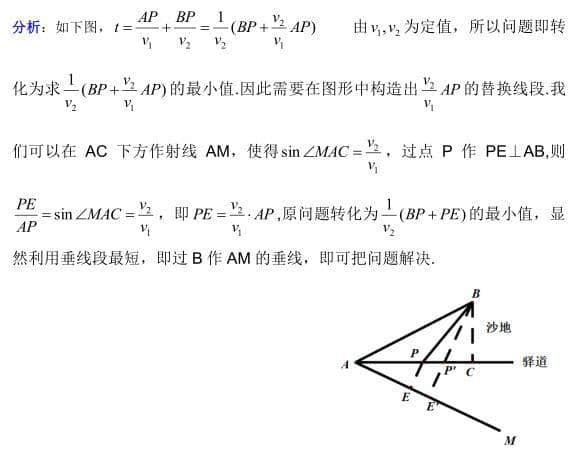
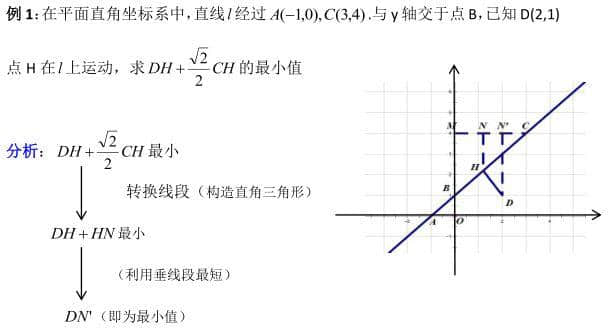
思路：将直线的函数表达式求出，利用L与坐标轴所夹锐角为45°，进而将

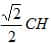
转化为HN , 即：利用垂线段最短

注：所要相加的两条线段位于L的异侧

2．如图，一条笔直的公路穿过草原，公路边有一消防站A，距离公路5千米的地方有一居民点B，A、B的直线距离是13千米．一天，居民点B着火，消防员受命欲前往救火，若消防车在公路上的最快速度是80千米/小时，而在草地上的最快速度是40千米/小时，则消防车在出发后最快经过 小时可到达居民点B．